Problem Statement:
Given the root of a binary tree, split the binary tree into two subtrees by removing one edge such that the product of the sums of the subtrees is maximized.
Return the maximum product of the sums of the two subtrees. Since the answer may be too large, return it modulo 109 + 7.
Note that you need to maximize the answer before taking the mod and not after taking it.
Example 1
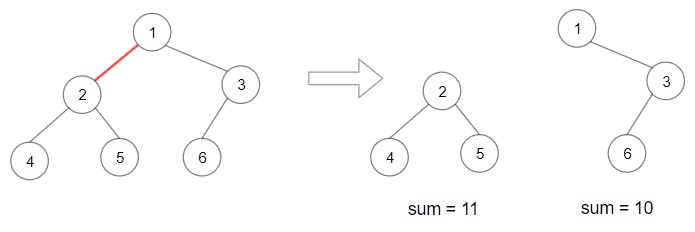
Input: root = [1,2,3,4,5,6]
Output: 110
Explanation: Remove the red edge and get 2 binary trees with sum 11 and 10. Their product is 110 (11*10)
Example 2
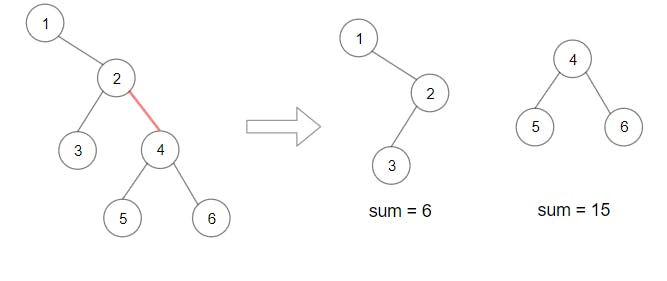
Input: root = [1,null,2,3,4,null,null,5,6]
Output: 90
Explanation: Remove the red edge and get 2 binary trees with sum 15 and 6.Their product is 90 (15*6)
Example 3:
Input: root = [2,3,9,10,7,8,6,5,4,11,1]
Output: 1025
Example 4:
Input: root = [1,1]
Output: 1
Constraints:
- The number of nodes in the tree is in the range [2, 5 * 104].
- 1 <= Node.val <= 104
Problem Solving Approach
From the given examples we understand that given a tree, we need to find the max of sum of nodes of the tress that we get as a result of the splitting.
This means having the sum of all nodes under an arbitrary node n will help us to find this product if the tree is split above n node. To explain more on this, consider the given example :
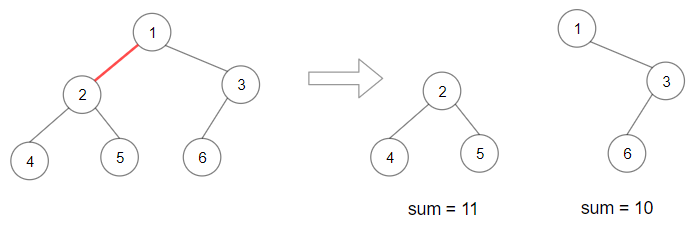
If we had somehow stored the value of the sum of all sub nodes for a given node (Here for node 2 we would store 11 and for the root node `1 we would store 21), then we can easily compute the product when breaking the tree at a particular node by doing the following:
- In the first parse of the tree, calculate the sum of itself and all the nodes below it.
- Get the sum of the subtree under the point where the tree was broken. Let's call this value
n - The sum of the rest of the tree would then become
sum_at_root_node - n. Let's call thism - Return the product of
mandnas modulo 109 + 7
Implementation
Below is the implementation for a function that returns the sum for all nodes of the subtree with the given node as the root node:
Integer generateSumAtNodes(TreeNode node, Map<TreeNode, Integer> map) {
// Initialize sum of left and right subtree as zero
Integer left = 0;
Integer right = 0;
// If left subtree exists find the sum of all nodes on the left side
if(node.left != null) {
left = generateSumAtNodes(node.left, map);
}
// If right subtree exists find the sum of all nodes on the left side
if(node.right != null) {
right = generateSumAtNodes(node.right, map);
}
// Save the sum of all nodes including and under the given node and return the sum
map.put(node, node.val + left + right);
return map.get(node);
}
Here a map is used to keep track of all the nodes and the respective values for the sum of that subtree.
After parsing the tree to find the sum of nodes at each node, we need to find the possible values of the product of sums of a splitted binary tree nodes. The implementation of this function would look something like this:
int getMaxProduct(Map<TreeNode, Integer> map, TreeNode root) {
long max = 0;
long mod=(long) 1e9+7;
long total = map.get(root);
// Parse the tree and find the product of sum of splitted binary tree at
// each node and return the max value
for(TreeNode node: map.keySet()) {
max = Math.max((map.get(node) * (total - map.get(node))), max);
}
return (int)(max % mod);
}
Here as you can see, we are using the difference between the total sum of all nodes and the sum at an arbitrary node to find the two values for which we need to find the product. This is done at each node and the maximum product is returned at the end.
Now we plug in these two functions into our solution class as follows:
import java.util.*;
class Solution {
public int maxProduct(TreeNode root) {
Map<TreeNode, Integer> map = new HashMap<TreeNode, Integer>();
generateSumAtNodes(root, map);
return getMaxProduct(map, root);
}
Integer generateSumAtNodes(TreeNode node, Map<TreeNode, Integer> map) {
Integer left = 0;
Integer right = 0;
if(node.left != null) {
left = generateSumAtNodes(node.left, map);
}
if(node.right != null) {
right = generateSumAtNodes(node.right, map);
}
map.put(node, node.val + left + right);
return map.get(node);
}
int getMaxProduct(Map<TreeNode, Integer> map, TreeNode root) {
long max = 0;
long mod=(long) 1e9+7;
long total = map.get(root);
for(TreeNode node: map.keySet()) {
max = Math.max((map.get(node) * (total - map.get(node))), max);
}
return (int)(max % mod);
}
}
